Розв'язуємо задачі!

9 клас

Рух тіла по похилій площині

Задачі не лише прочитати, але й розібратися з їх розв’язуванням та переписати у робочий зошит!!!!

Задача № 1

Вантаж масою 30 кг знаходиться на похилій площині з кутом нахилу 20⁰. Яку силу треба прикласти до вантажу вздовж схилу, щоб: а) витягти вантаж нагору; б) стягнути вантаж униз? Коефіцієнт тертя вантажу об площину дорівнює 0,4.

Розв’язування

Задача а)

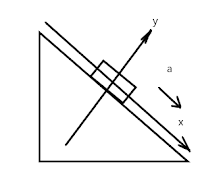
1). Зробимо малюнок тіла на похилій площині. У тіла, що піднімається або спускається з похилої площини, змінюються дві координати: х та у, тому через тіло проводять дав осі руху.

2). Проведемо через тіло осі руху: вісь Х паралельно до площини, вісь У – перпендикулярно до осі Х, та позначимо напрямок прискорення. Вісь Х напрямлена у бік руху тіла.

3). Позначимо сили, що діють на тіло: сила тяжіння напрямлена вертикально вниз; сила тяги -  вздовж осі Х у бік руху тіла (у нашому випадку вздовж Х вгору); сила тертя – вздовж осі Х проти руху (вниз); сила реакції опори – завжди перпендикулярна опорі і напрямлена від неї. Сили тяги, тертя і реакції опори напрямлені вздовж осей, тому дуже легко можна перейти до їх проекцій; сила тяжіння напрямлена під кутом і до осі Х, і до осі У, тому розкладаємо цю силу на складові вздовж осей. З кінця вектору сили тяжіння опускаємо перпендикуляри на осі Х та У. Складові сили тяжіння прикладені до тіла (починаються з центра тіла) і закінчуються перпендикулярами (дивись малюнок). На малюнку позначено однакові кути α.

4). Записуємо другий закон Ньютона у векторній формі для кожної осі руху.

        →    →   →     →

ОХ: ma = F + Fт + mg_x

        →    →    →

OУ: ma = N + mg_у

5). Від векторів перейдемо до їх проекцій на задані осі руху:

ОХ: ma_х = F - Fт - mg_x

OУ: ma_у = N - mg_у

6). Спочатку розв’яжемо рівняння відносно осі У, враховуючи, що вздовж осі У тіло не рухається, тому завжди прискорення а_у дорівнює нулю. Добуток будь-якого числа на нуль теж дорівнює нулю, тоді:

0 = N - mg_у, звідки N = mg_у, де з прямокутного трикутника (дивись малюнок) mg_у = mg∙Cosα, тоді N = mg∙Cosα. Тепер ми можемо виразити ситу тертя F_т = μN = μ mg∙Cosα. Рівняння відносно осі У розв’язується однаково для будь-якої задачі на похилу площину, цей розв’язок можна переписувати від задачі до задачі. Як тільки ми визначили силу тертя, переходимо до розв’язування задачі відносно осі Х. Проекція прискорення на вісь Х дорівнює модулю прискорення, з яким рухається тіло:

ma = F - Fт - mg_x

Але у нашій задачі ми витягуємо тіло без прискорення (умова), тобто а = 0. Проекція сили тяжіння на вісь Х визначається з прямокутного трикутника (дивись малюнок):

mg_x = mg∙Sinα

Підставимо значення прискорення, сили тертя і проекції сили тяжіння на вісь Х у рівняння, отримаємо:

0 = F - μ mg∙Cosα - mg∙Sinα, звідки

F = μ mg∙Cosα + mg∙Sinα

Винесемо у рівнянні за дужки спільний множник mg, отримаємо:

F = mg∙(μCosα + Sinα)

Підставимо значення величин: F = 30∙10∙(0,4∙Cos 20 + Sin 20) = 215 Н.

Задача б)

1). Зробимо малюнок тіла на похилій площині. У тіла, що піднімається або спускається з похилої площини, змінюються дві координати: х та у, тому через тіло проводять дав осі руху.

2). Проведемо через тіло осі руху: вісь Х паралельно до площини, вісь У – перпендикулярно до осі Х, та позначимо напрямок прискорення. Вісь Х напрямлена у бік руху тіла.

3). Позначимо сили, що діють на тіло: сила тяжіння напрямлена вертикально вниз; сила тяги -  вздовж осі Х у бік руху тіла (у нашому випадку вздовж Х вниз); сила тертя – вздовж осі Х проти руху (вгору); сила реакції опори – завжди перпендикулярна опорі і напрямлена від неї. Сили тяги, тертя і реакції опори напрямлені вздовж осей, тому дуже легко можна перейти до їх проекцій; сила тяжіння напрямлена під кутом і до осі Х, і до осі У, тому розкладаємо цю силу на складові вздовж осей. З кінця вектору сили тяжіння опускаємо перпендикуляри на осі Х та У. Складові сили тяжіння прикладені до тіла (починаються з центра тіла) і закінчуються перпендикулярами (дивись малюнок). На малюнку позначено однакові кути α.

4). Записуємо другий закон Ньютона у векторній формі для кожної осі руху.

        →    →   →     →

ОХ: ma = F + Fт + mg_x

        →    →    →

OУ: ma = N + mg_у

5). Від векторів перейдемо до їх проекцій на задані осі руху:

ОХ: ma_х = F - Fт + mg_x

OУ: ma_у = N - mg_у

6). Спочатку розв’яжемо рівняння відносно осі У, враховуючи, що вздовж осі У тіло не рухається, тому завжди прискорення а_у дорівнює нулю. Добуток будь-якого числа на нуль теж дорівнює нулю, тоді:

0 = N - mg_у, звідки N = mg_у, де з прямокутного трикутника (дивись малюнок) mg_у = mg∙Cosα, тоді N = mg∙Cosα. Тепер ми можемо виразити ситу тертя F_т = μN = μ mg∙Cosα. Рівняння відносно осі У розв’язується однаково для будь-якої задачі на похилу площину, цей розв’язок можна переписувати від задачі до задачі. Як тільки ми визначили силу тертя, переходимо до розв’язування задачі відносно осі Х. Проекція прискорення на вісь Х дорівнює модулю прискорення, з яким рухається тіло:

ma = F - Fт + mg_x

Але у нашій задачі ми стягуємо тіло без прискорення (умова), тобто а = 0. Проекція сили тяжіння на вісь Х визначається з прямокутного трикутника (дивись малюнок):

mg_x = mg∙Sinα

Підставимо значення прискорення, сили тертя і проекції сили тяжіння на вісь Х у рівняння, отримаємо:

0 = F - μ mg∙Cosα + mg∙Sinα, звідки

F = μ mg∙Cosα - mg∙Sinα

Винесемо у рівнянні за дужки спільний множник mg, отримаємо:

F = mg∙(μCosα - Sinα)

Підставимо значення величин: F = 30∙10∙(0,4∙Cos 20 - Sin 20) = 10 Н.

Задача № 2

Автомобіль масою 4 т рухається вгору з прискоренням 0,2 м/с². Знайти силу тяги, якщо ухил дорівнює 0,02 і коефіцієнт опору 0,04.

Розв’язування

Ухил дорівнює синусу кута нахилу площини до горизонту, тобто Sinα = 0,02. Якщо ухил малий, менший за 0,1, то Cosα можна вважати приблизно дорівнюючим одиниці, тобто Cosα = 1.

1). Зробимо малюнок тіла на похилій площині. У тіла, що піднімається або спускається з похилої площини, змінюються дві координати: х та у, тому через тіло проводять дав осі руху.

2). Проведемо через тіло осі руху: вісь Х паралельно до площини, вісь У – перпендикулярно до осі Х, та позначимо напрямок прискорення. Вісь Х напрямлена у бік руху тіла.

3). Позначимо сили, що діють на тіло: сила тяжіння напрямлена вертикально вниз; сила тяги -  вздовж осі Х у бік руху тіла (у нашому випадку вздовж Х вгору); сила тертя – вздовж осі Х проти руху (вниз); сила реакції опори – завжди перпендикулярна опорі і напрямлена від неї. Сили тяги, тертя і реакції опори напрямлені вздовж осей, тому дуже легко можна перейти до їх проекцій; сила тяжіння напрямлена під кутом і до осі Х, і до осі У, тому розкладаємо цю силу на складові вздовж осей. З кінця вектору сили тяжіння опускаємо перпендикуляри на осі Х та У. Складові сили тяжіння прикладені до тіла (починаються з центра тіла) і закінчуються перпендикулярами (дивись малюнок). На малюнку позначено однакові кути α.

4). Записуємо другий закон Ньютона у векторній формі для кожної осі руху.

        →    →   →     →

ОХ: ma = F + Fт + mg_x

        →    →    →

OУ: ma = N + mg_у

5). Від векторів перейдемо до їх проекцій на задані осі руху:

ОХ: ma_х = F - Fт - mg_x

OУ: ma_у = N - mg_у

6). Спочатку розв’яжемо рівняння відносно осі У, враховуючи, що вздовж осі У тіло не рухається, тому завжди прискорення а_у дорівнює нулю. Добуток будь-якого числа на нуль теж дорівнює нулю, тоді:

0 = N - mg_у, звідки N = mg_у, де з прямокутного трикутника (дивись малюнок) mg_у = mg∙Cosα, тоді N = mg∙Cosα. Тепер ми можемо виразити ситу тертя F_т = μN = μ mg∙Cosα. Рівняння відносно осі У розв’язується однаково для будь-якої задачі на похилу площину, цей розв’язок можна переписувати від задачі до задачі. Як тільки ми визначили силу тертя, переходимо до розв’язування задачі відносно осі Х. Проекція прискорення на вісь Х дорівнює модулю прискорення, з яким рухається тіло:

ma = F - Fт - mg_x

Проекція сили тяжіння на вісь Х визначається з прямокутного трикутника (дивись малюнок):

mg_x = mg∙Sinα

Підставимо значення прискорення, сили тертя і проекції сили тяжіння на вісь Х у рівняння, отримаємо:

ma = F - μ mg∙Cosα - mg∙Sinα, звідки

F = μ mg∙Cosα + mg∙Sinα + ma

Винесемо у рівнянні за дужки спільний множник m, отримаємо:

F = m∙(μgCosα + gSinα + a)

Підставимо значення величин: F = 4∙10³∙(0,04∙10∙1 + 10∙0,02 + 0,2) = 3,2∙10³ Н = 3,2 кН.

Задача № 3

З яким прискорення ковзає брусок по похилій площині з кутом нахилу 30⁰ при коефіцієнті тертя 0,2?

Розв’язування

1). Зробимо малюнок тіла на похилій площині. У тіла, що піднімається або спускається з похилої площини, змінюються дві координати: х та у, тому через тіло проводять дав осі руху.

2). Проведемо через тіло осі руху: вісь Х паралельно до площини, вісь У – перпендикулярно до осі Х, та позначимо напрямок прискорення. Вісь Х напрямлена у бік руху тіла.

3). Позначимо сили, що діють на тіло: сила тяжіння напрямлена вертикально вниз; сили тяги немає, бо брусок сам зісковзує з площини; сила тертя – вздовж осі Х проти руху (вгору); сила реакції опори – завжди перпендикулярна опорі і напрямлена від неї. Сили тертя і реакції опори напрямлені вздовж осей, тому дуже легко можна перейти до їх проекцій; сила тяжіння напрямлена під кутом і до осі Х, і до осі У, тому розкладаємо цю силу на складові вздовж осей. З кінця вектору сили тяжіння опускаємо перпендикуляри на осі Х та У. Складові сили тяжіння прикладені до тіла (починаються з центра тіла) і закінчуються перпендикулярами (дивись малюнок). На малюнку позначено однакові кути α.

4). Записуємо другий закон Ньютона у векторній формі для кожної осі руху.

        →       →     →

ОХ: ma =  Fт + mg_x

        →    →    →

OУ: ma = N + mg_у

5). Від векторів перейдемо до їх проекцій на задані осі руху:

ОХ: ma_х =  - Fт + mg_x

OУ: ma_у = N - mg_у

6). Спочатку розв’яжемо рівняння відносно осі У, враховуючи, що вздовж осі У тіло не рухається, тому завжди прискорення а_у дорівнює нулю. Добуток будь-якого числа на нуль теж дорівнює нулю, тоді:

0 = N - mg_у, звідки N = mg_у, де з прямокутного трикутника (дивись малюнок) mg_у = mg∙Cosα, тоді N = mg∙Cosα. Тепер ми можемо виразити ситу тертя F_т = μN = μ mg∙Cosα. Рівняння відносно осі У розв’язується однаково для будь-якої задачі на похилу площину, цей розв’язок можна переписувати від задачі до задачі. Як тільки ми визначили силу тертя, переходимо до розв’язування задачі відносно осі Х. Проекція прискорення на вісь Х дорівнює модулю прискорення, з яким рухається тіло:

ma = - Fт + mg_x

Проекція сили тяжіння на вісь Х визначається з прямокутного трикутника (дивись малюнок):

mg_x = mg∙Sinα

Підставимо значення прискорення, сили тертя і проекції сили тяжіння на вісь Х у рівняння, отримаємо:

ma = mg∙Sinα - μ mg∙Cosα 

Скоротимо обидві частини рівняння на масу та винесемо спільний множник g за дужки, отримаємо:

a = g∙(Sinα - μ∙Cosα)

Підставимо значення величин: а = 10∙(0,5 – 0,2∙0,866) = 3,3 м/с².

Домашнє завдання

Розв’язати задачі

Задачі сфотографувати та відправити за адресою omichka@ukr.net

Задача № 1

На похилій площині завдовжки 13 м і заввишки 5 м лежить вантаж масою 26 кг. Коефіцієнт тертя дорівнює 0,5. Яку силу треба прикласти до вантажу вздовж схилу, щоб: а) витягти вантаж нагору; б) стягнути вантаж униз?

Розв’язування

ЗАДАЧА РОЗВЯЗУЄТЬСЯ, ЯК І ЗАДАЧА № 1 З ПОЯСНЕННЯ! Єдине, чим відрізняється ця задача – у ній не вказано кут нахилу похилої площини, але синус та косинус можна знайти за визначенням з прямокутного трикутника, у якого відомі катет і гіпотенуза.

Задача № 2

Потяг масою 3000 т рухається вниз під ухил, що дорівнює 0,003. Коефіцієнт опору руху дорівнює 0,008. З яким прискоренням рухається потяг. Якщо сила тяги локомотива дорівнює 300 кН?

10 клас

Термодинаміка. Робота газу

Задачі не лише прочитати, але й розібратися з їх розв’язуванням та переписати у робочий зошит!!!!

Задача № 1

У вертикальному циліндрі під поршнем знаходиться повітря масою 29 г. Яку роботу виконає повітря при підвищенні температури на 100 К?

Розв’язування

Робота газу визначається за формулою A = PΔV (1). Для розв’язування цієї задачі знов використовуємо рівняння Менделєєва – Клапейрона: PV = mRT/M. Якщо змінюється об’єм, то відповідно (за задачею) змінюється і температура, тобто PΔV = mRΔT/M (2). Підставимо вираз (2) у формулу (1), отримаємо: А =  mRΔT/M. Підставимо значення величин, враховуючи, що молярна маса повітря М = 29 г/моль, отримаємо:

А = (29∙8,31∙100)/29 = 831 Дж.

Задача № 2

У вертикально розташованому циліндрі з площею основи 1 дм² під поршнем масою 10 кг, який ковзає без тертя, знаходиться повітря. Під час ізобарного нагрівання повітря поршень піднявся на 20 см. Яку роботу виконало повітря, якщо зовнішній тиск 100 кПа?

Розв’язування

Робота газу визначається за формулою A = PΔV (1), де об’єм циліндра можна знайти за формулою V = Sh, звідки зміна об’єму ΔV = SΔh (2). Тиск на повітря, що знаходиться під поршнем, складається з двох компонентів: атмосферного тиску та тиску поршня. Тиск поршня – це відношення сили тяжіння F = mg до площі поршня, тобто P = P₀ + mg/S (3), де P₀ – атмосферний тиск. Підставимо вирази (2) та (3) у формулу (1), отримаємо:

А = (P₀ + mg/S)SΔh

де площа поршня S = 1 дм² = (1 дм = 10^-1 м) = 10^-2 м² , зміна висоти Δh = 20 см = 0,2 м. Підставимо значення величин у формулу, отримаємо:

А = (100∙10³ + 100/10^-2)∙ 10^-2 ∙0,2 = 110∙10³∙10^-2 ∙0,2 = 220 Дж.

Задача № 3

Температура в кімнаті об’ємом 70 м³ була 280 К. Після того, як протопили піч, температура піднялась до 296 К. Знайти роботу повітря під час розширення, якщо тиск постійний і дорівнює 100 кПа.

Розв’язування

Робота газу визначається за формулою A = PΔV = P(V₂ – V₁) (1), де V₁= 70 м³. Для того, щоб визначити кінцевий об’єм повітря V₂, використаємо газовий закон Гей-Люссака для ізобарного процесу:

V₁/T₁ = V₂/T₂, звідки V₂ = V₁T₂/T₁ (2)

Підставимо вираз (2) у формулу (1), отримаємо:

А = Р(V₁T₂/T₁ - V₁) = Р V₁(T₂/T₁ – 1).

Підставимо значення величин, отримаємо (враховуючи, що 100 кПа = 10⁵ Па):

А = 10⁵∙70∙(296/280 – 1) = 4∙10⁵ Дж = 400 кДж.

Задача № 4

При нагріванні повітря в циліндрі поршень масою 5 кг і площею 50 см² перемістився на 15 см. Яку роботу виконало повітря, якщо поршень переміщався: а) горизонтально;

 б) вертикально вгору; в) вертикально вниз?

Розв’язування

Робота газу визначається за формулою A = PΔV (1), де об’єм циліндра можна знайти за формулою V = Sh, звідки зміна об’єму ΔV = SΔh (2). Тиск на повітря, що знаходиться під поршнем, складається з двох компонентів: атмосферного тиску та тиску поршня. Тиск поршня – це відношення сили тяжіння F = mg до площі поршня, тобто P = P₀ + mg/S (3), де P₀ – атмосферний тиск. Підставимо вирази (2) та (3) у формулу (1), отримаємо:

А = (P₀ + mg/S)SΔh

де площа поршня S = 50 см² = (1 см = 10^-2 м) = 50∙10^-4 м² , зміна висоти Δh залежить від умови задачі: а) поршень рухається горизонтально, висота не змінюється, тобто Δh = 0, тоді робота газу А = 0; б) якщо поршень рухається вертикально вгору, то Δh = 15 см = 0,15 м, тоді

А = (100∙10³ + 50/50∙10^-4)∙ 50∙10^-4 ∙0,15 = 110∙10³∙50∙10^-4 ∙0,15 = 82,5 Дж; в) якщо поршень рухається вертикально вниз, то висота зменшується, тобто Δh = - 15 см = - 0,15 м, тоді

А = (100∙10³ + 50/50∙10^-4)∙ 50∙10^-4 ∙(-0,15) = 110∙10³∙50∙10^-4 ∙(-0,15) = - 82,5 Дж.

Домашнє завдання

Розв’язати задачі

Задачі сфотографувати та відправити за адресою omichka@ukr.net

Задача № 1

Яку роботу виконає газ при ізобарному нагріванні на 50 К, якщо кількість речовини в газі дорівнює 5 моль?

Задача № 2 

При нагріванні повітря в циліндрі поршень масою 15 кг і площею 100 см² перемістився на

5 см. Яку роботу виконало повітря, якщо поршень переміщався вертикально вгору?

Задача № 3

Температура в кімнаті об’ємом 50 м³  піднялась від 15⁰ С до 25⁰ С. Знайти роботу повітря під час розширення, якщо атмосферний  тиск постійний і дорівнює 100 кПа.

11 клас!!!

 УВАГА! Сьогодні, у ЧЕТВЕР 9 КВІТНЯ о 13 ГОДИНІ ви будете писати контрольну роботу по фотоефекту. Роботу виконуєте на листку паперу, фотографуєте і відправляєте за адресою 

omichkanatali@gmail.com.