1. Задачі на інтерференцію та дифракцію світла. Використовуємо
формули: умова максимумів Δd = kλ, де k – ціле
число 0; 1; 2; … Умова мінімумів Δd = (2k + 1)λ/2,
умова максимумів для дифракційної гратки dsinφ = kλ, період
дифракційної гратки d = L/N, де L – одиниця довжини або довжина гратки, N – кількість штрихів.
Задача №
1059
Два когерентних джерела, відстань між якими становить 1 мм,
випускають монохроматичне світло з довжиною хвилі 600 нм. Визначити, на якій
відстані від центрального максимуму буде максимум першого порядку, якщо
відстань джерел від екрана дорівнює 4 м.
Розв’язування
Спочатку обов’язково зробимо малюнок, на якому позначимо відомі
величини. Нехай маленька відстань між джерелами буде позначатися l, а велика відстань між джерелами та екраном – L.
Задача № 2
Два когерентних джерела, відстань між якими становить 2 мм,
випускають монохроматичне світло з довжиною хвилі 500 нм. Визначити відстань від джерел до екрана, якщо максимум
третього порядку знаходиться на відстані
4,5 мм від центрального максимуму.
Розв’язування
Спочатку обов’язково зробимо малюнок, на якому позначимо відомі
величини. Нехай маленька відстань між джерелами буде позначатися l, а велика відстань між джерелами та екраном – L.
Задача №
1066
Дифракційна гратка має 120 штрихів на 1 мм. Визначити довжину хвилі
монохроматичного світла, що падає на гратку, якщо кут між двома спектрами
першого порядку становить 80.
Розв’язування
Період дифракційної гратки d = L/N = 1∙10-3/120
(м). З умови максимумів dsinφ = kλ
визначаємо λ = dsinφ/k, де φ
– це кут між центральним максимумом та максимумом першого порядку, а в задачі
відомий кут між максимумами перших порядків (зліва і справа від центрального),
тому φ = 8/2 = 40. Підставимо значення величин λ = (1∙10-3∙sin40)/(120∙1) = 5,8∙10-7
м.
Задача №
1067
Визначити кут відхилення зеленого світла (λ = 0,55
мкм) у спектрі першого порядку, утвореному за допомогою дифракційної гратки,
період якої 0,02 мм.
Розв’язування
З умови максимумів dsinφ = kλ
визначаємо sinφ
= kλ/d. Підставимо значення величин sinφ
= 1∙5,5∙10-7/2∙10-5 = 0,0275, звідки φ = arcsin(0,0275) = 1,60.
Задача №
1069
Який період має дифракційна гратка, що опромінюється світлом з
довжиною хвилі 0,76 мкм, якщо на екрані, віддаленому від неї на 1 м, відстань
між спектрами першого порядку дорівнює 15,2 см?
Розв’язування
Спочатку обов’язково зробимо малюнок, на якому позначимо відомі
величини. Відстань до екрану позначимо L, відстань між центральним максимумом та
максимумом першого порядку позначимо x.
Умова максимумів dsinφ = kλ, але для максимумом першого порядку кут φ такий малий (дивитись попередню задачу), що можна замінити sinφ на tgφ, тоді dtgφ = kλ. З трикутника tgφ = x/L, тоді dx/L = kλ, звідки d = kλL/x. Відстань х – відстань між центральним максимумом та максимумом першого порядку, а нам відома відстань між двома максимумами першого порядку (зліва і справа від центрального), тому х = 15,2 см/2 = 7,6 см. Підставимо значення величин
d
= (1∙7,6∙10-7∙1)/(7,6∙10-2) = 1∙10-5 м.
Задача №
1070
Яку ширину має весь спектр першого порядку (довжини хвиль лежать у
межах від 0,38 до 0,76 мкм), утворений на екрані, віддаленому на 3 м від
дифракційної гратки з періодом 0,01 мм?
Розв’язування
Спочатку обов’язково зробимо малюнок, на якому позначимо відомі
величини. Відстань до екрану позначимо L, відстань між центральним максимумом та
максимумом першого порядку позначимо x, для
фіолетового кольору хф, для червоного кольору хч. Ширина
всього спектру випромінювання Х = хч – хф (1).
Умова максимумів dsinφ = kλ, але для максимумом першого порядку кут φ такий малий (дивитись попередню задачу), що можна замінити sinφ на tgφ, тоді dtgφ = kλ. З трикутника tgφ = x/L, тоді dx/L = kλ, звідки х = kλL/d, тоді хч = kλчL/d, хф = kλфL/d (2). Підставимо (2) в (1), отримаємо
Х = kλчL/d - хф = kλфL/d = kL(λч – λф)/d. Підставимо значення величин
Х =
(1∙3∙(7,6∙10-7 – 3,8∙10-7))/(1∙10-5) = (1∙3∙
3,8∙10-7)/(1∙10-5) = 11,4∙10-2 м = 11,4 см.
2. Задачі на заломлення. Використовуємо формулу закону заломлення:
sinα/sinβ = n, n = n1/n2.
Задача
№ 1
Під яким кутом повинен падати промінь на скло, щоб між
заломленим та відбитим променями був кут 1200?
Розв’язування
Зробимо малюнок, намалюємо падаючий, відбитий та
заломлений промені.
β = 600 – α. Підставимо значення кута β у формулу sinα/sinβ = n, тоді
sinα/sin(600 – α). Розкладемо синус різниці кутів sin(600 – α) за правилом, тоді sinα/(sin600cosα – cos600sinα) = sinα/(0,866cosα – 0,5sinα) = 1,6. З цього рівняння sinα = 1,6∙(0,866cosα – 0,5sinα) або sinα = 1,39cosα – 0,8sinα, тоді
1,8sinα = 1,39cosα. Поділимо ліву і праву частини рівняння на cosα, отримаємо: 1,8tgα = 1,39, звідки tgα = 0,7722. Кут α = arctg(0,7722) = 380.
Задача
№ 2
Промінь падає під кутом 500 на трикутну
призму із заломним кутом 600. Визначити кут заломлення променю під
час виходу з призми.
Розв’язування
Зробимо малюнок призми, позначимо поширення світлових
променів.
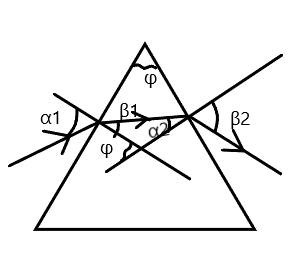
Кут α1 – кут падіння на першу грань призми. Промінь переходить з повітря у скло, тому кут заломлення менший за кут падіння. Обчислимо його з формули sinα1/sinβ1 = n, звідки sinβ1 = sinα1/n. Підставимо значення величин:
sinβ1 = sin500/1,6 = 0,4788, β1 = arcsin(0,4788) = 290. Заломний кут – це кут у вершині призми. Позначимо його φ. Кут α2 визначимо з трикутника, що намальований всередині призми: лівий кут – β1, правий кут – α2, нижній кут – (1800-φ). Сума трьох кутів трикутника дорівнює 1800, тому
α2 + β1 + (180 – φ) = 1800 або α2 = φ - β1 = 600 – 290 = 310. Світловий промінь, що виходить з призми, переходить із скла у повітря, тому β2 > α2. Обчислимо α2 з формули sinα2/sinβ2 = 1/n (бо перехід з середовища більш густого у менш густе), звідки sinβ2 = nsinα2. Підставимо значення величин: sinβ2 = 1,6∙sin310 = 0,8241 або β2 = arcsin(0,8241) = 55,50.





Немає коментарів:
Дописати коментар